Số Chính Phương là Gì? Định Nghĩa, Tính Chất và Bài Tập Vận Dụng

Số chính phương là một khái niệm quan trọng trong toán học, đặc biệt là ở bậc trung học cơ sở. Bài viết này sẽ giải đáp toàn bộ thắc mắc của bạn về số chính phương, từ định nghĩa, tính chất, cách nhận biết, cho đến các dạng bài tập thường gặp. Cùng tìm hiểu xem số 0 có phải là số chính phương không nhé!

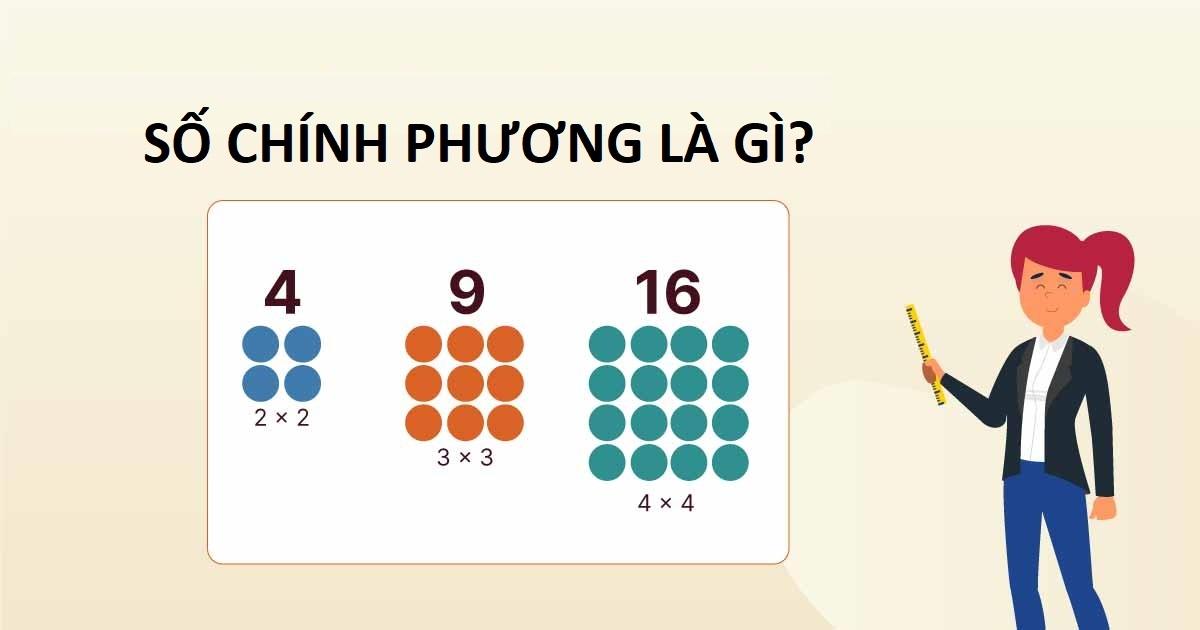Số chính phương là gì?

Bạn đã biết bước đầu tiên trong quy trình chế tạo cơ khí là gì chưa?

Số Chính Phương là Gì? Các Đặc Tính Cơ Bản

Định nghĩa số chính phương

Số chính phương là số nguyên dương có thể biểu diễn dưới dạng bình phương của một số nguyên. Nói cách khác, một số chính phương là kết quả của phép nhân một số nguyên với chính nó. Ví dụ, 4 là số chính phương vì 4 = 2 x 2, và 9 là số chính phương vì 9 = 3 x 3.

Ngược lại, số 5 và 7 không phải là số chính phương vì không có số nguyên nào nhân với chính nó bằng 5 hoặc 7.

Một số số chính phương đầu tiên là: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100,…

Đặc tính của số chính phương

Đặc tính của các số chính phương

Vậy đặc tính của các số chính phương là gì? Dưới đây là một số đặc điểm quan trọng:

• Công thức: Số chính phương được biểu diễn dưới dạng n², với n là một số nguyên.
• Tổng các số lẻ liên tiếp: Mọi số chính phương đều có thể được viết thành tổng của các số lẻ liên tiếp bắt đầu từ 1. Ví dụ: 4 = 1 + 3; 9 = 1 + 3 + 5; 16 = 1 + 3 + 5 + 7.
• Chữ số tận cùng: Chữ số tận cùng của một số chính phương chỉ có thể là 0, 1, 4, 5, 6 hoặc 9.
• Tính chất chia hết: Nếu một số chính phương chia hết cho một số nguyên tố p, thì nó cũng chia hết cho p². Ví dụ, nếu một số chính phương chia hết cho 3, thì nó cũng chia hết cho 9 (3²).
• Hình học: Số chính phương có thể được biểu diễn bằng các hình vuông, với mỗi điểm trên hình vuông đại diện cho một số chính phương và độ dài cạnh bằng căn bậc hai của số đó.

Bạn có biết ba yếu tố quyết định thành bại của chuyển đổi số là gì không?

Số Chính Phương Nhỏ Nhất

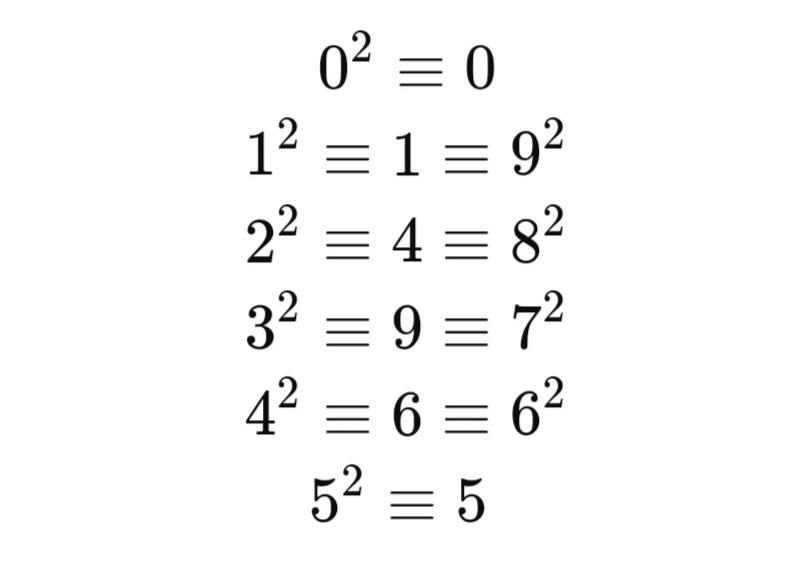Số chính phương nhỏ nhất

Số chính phương nhỏ nhất phụ thuộc vào tập số đang xét. Nếu chỉ xét các số nguyên dương, số chính phương nhỏ nhất là 1 (1² = 1). Tuy nhiên, nếu xét cả số 0, thì số chính phương nhỏ nhất là 0 (0² = 0).

Số Chính Phương Lớn Nhất trong Phạm Vi Số Nguyên Tố

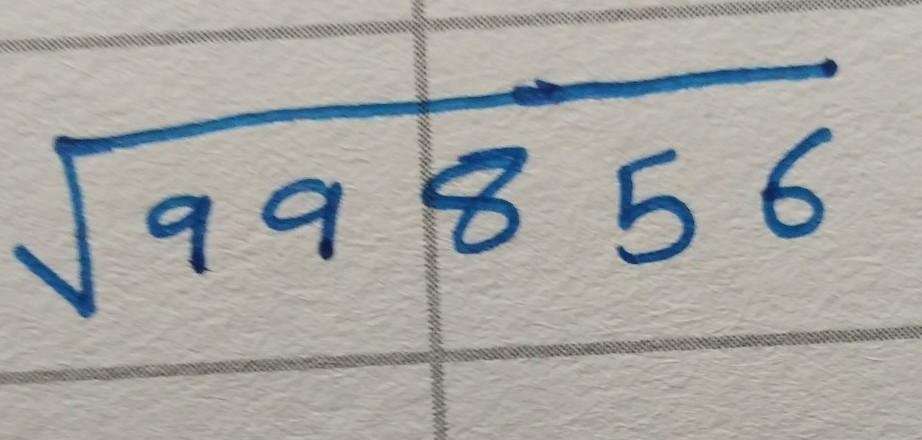Số chính phương lớn nhất trong phạm vi các số tự nhiên dương là 99856

Trong một phạm vi số nguyên tố nhất định, số chính phương lớn nhất chính là bình phương của số nguyên tố lớn nhất trong phạm vi đó. Ví dụ, trong phạm vi số nguyên tố có một chữ số (từ 2 đến 7), số nguyên tố lớn nhất là 7, và số chính phương lớn nhất là 49 (7² = 49). Vậy chỉ số sản xuất công nghiệp là gì?

Cách Nhận Biết Số Chính Phương

Có nhiều cách để nhận biết một số có phải là số chính phương hay không:

Kiểm tra căn bậc hai

Nếu căn bậc hai của một số là một số nguyên, thì số đó là số chính phương.

Chữ số tận cùng

Như đã đề cập, số chính phương chỉ có thể kết thúc bằng 0, 1, 4, 5, 6 hoặc 9.

Phân tích thừa số nguyên tố

Một số là số chính phương nếu tất cả các số mũ trong phân tích ra thừa số nguyên tố của nó đều là số chẵn.

Sử dụng bảng số chính phương

Tra cứu bảng số chính phương để kiểm tra nhanh.

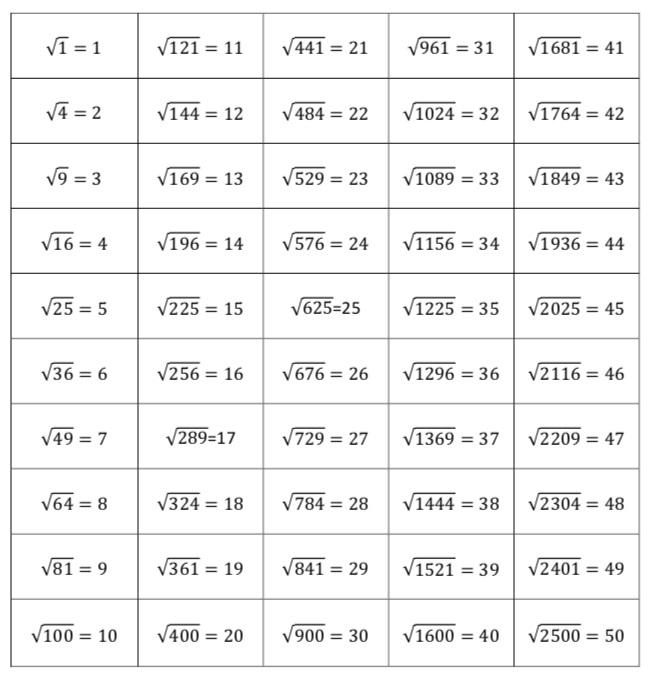Sử dụng bảng số chính phương

Bạn đã tìm hiểu về đường kính lưỡng đỉnh là gì chưa?

Sử dụng công cụ tính toán

Máy tính hoặc ứng dụng tính toán có thể giúp xác định nhanh chóng xem một số có phải là số chính phương hay không, đặc biệt là với các số lớn.

Một Số Dạng Bài Tập về Số Chính Phương

Dạng 1: Chứng minh số chính phương

Ví dụ: Chứng minh B = 4n⁴ + 4n³ + n² là số chính phương với mọi số nguyên dương n.

Lời giải: B = n²(4n² + 4n + 1) = n²(2n + 1)² = [n(2n + 1)]². Vì n(2n + 1) là số nguyên nên B là số chính phương.

Dạng 2: Tìm n sao cho một số là chính phương

Ví dụ: Tìm số tự nhiên n sao cho B = n² + 4n + 1 là số chính phương.

Lời giải: Đặt n² + 4n + 1 = b². Biến đổi thành (2n + 4)² – 4b² = 12, hay (2n + 4 + 2b)(2n + 4 – 2b) = 12. Xét các cặp số nguyên dương có tích bằng 12 và giải tìm n. Kết quả là n = 0.

Vậy nội dung phản ánh đầy đủ đặc trưng của chính phủ số là gì?