Công Thức Tính Thể Tích Khối Lăng Trụ và Bài Tập Vận Dụng [thể tích khối lăng trụ]

Việc nắm vững cách tính thể tích khối lăng trụ là kiến thức quan trọng trong hình học không gian, giúp học sinh giải quyết các bài tập và áp dụng vào thực tế. Bài viết này sẽ cung cấp đầy đủ thông tin về hình lăng trụ, các công thức tính toán liên quan và bài tập minh họa chi tiết.

Hình lăng trụ xuất hiện phổ biến trong cuộc sống, từ các công trình kiến trúc đến vật dụng hàng ngày. Hiểu rõ về hình lăng trụ giúp chúng ta phát triển tư duy không gian và giải quyết các vấn đề thực tiễn liên quan đến thể tích, diện tích. Việc ôn tập lại các khái niệm và công thức tính toán sẽ giúp các bạn học sinh dễ dàng chinh phục dạng bài này. Bên cạnh đó, bài viết còn cung cấp một số bài tập vận dụng, giúp bạn đọc củng cố kiến thức.

Định Nghĩa Các Loại Hình Lăng Trụ [hình lăng trụ]

Hình Lăng Trụ

Hình lăng trụ là hình đa diện gồm hai đáy là hai đa giác bằng nhau nằm trên hai mặt phẳng song song. Đáy của hình lăng trụ có thể là hình chữ nhật, hình vuông, hình bình hành, tam giác,… Các mặt bên là hình bình hành, các cạnh bên song song và bằng nhau.

Hình lăng trụ

• Hai đáy là hai đa giác bằng nhau nằm trong hai mặt phẳng song song.
• Các cạnh bên song song với nhau.
• Các mặt bên là hình bình hành.

Hình Lăng Trụ Đứng

Hình lăng trụ đứng là hình lăng trụ có các cạnh bên vuông góc với mặt đáy. Các mặt bên là hình chữ nhật. Chiều cao của hình lăng trụ đứng chính là độ dài của cạnh bên. Tên gọi của hình lăng trụ đứng dựa vào hình đa giác đáy, ví dụ: hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác,…

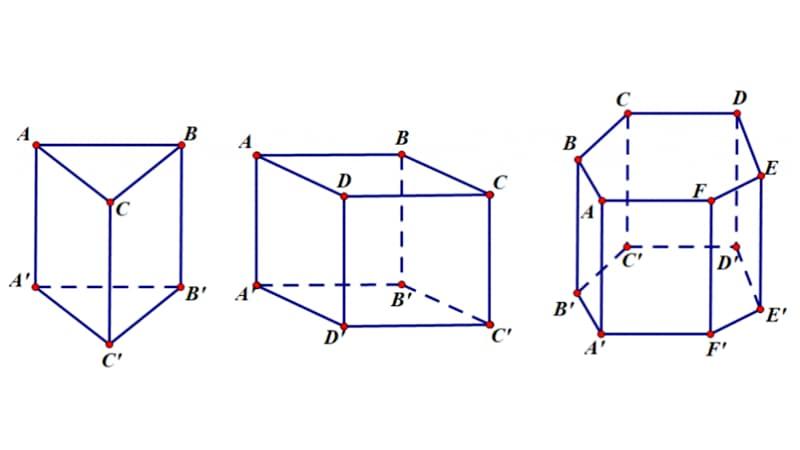Hình lăng trụ đứng

• Các cạnh bên vuông góc với đáy.
• Các mặt bên là hình chữ nhật.
• Hai mặt phẳng đáy song song với nhau.
• Chiều cao bằng độ dài cạnh bên.

Bạn đã bao giờ tự hỏi kỹ năng làm việc độc lập tiếng anh là gì chưa?

Hình Lăng Trụ Đều

Hình lăng trụ đều là hình lăng trụ đứng có đáy là đa giác đều. Các cạnh đáy bằng nhau và các mặt bên là hình chữ nhật vuông góc với mặt đáy. Ví dụ: hình lăng trụ tam giác đều, hình lăng trụ tứ giác đều,…

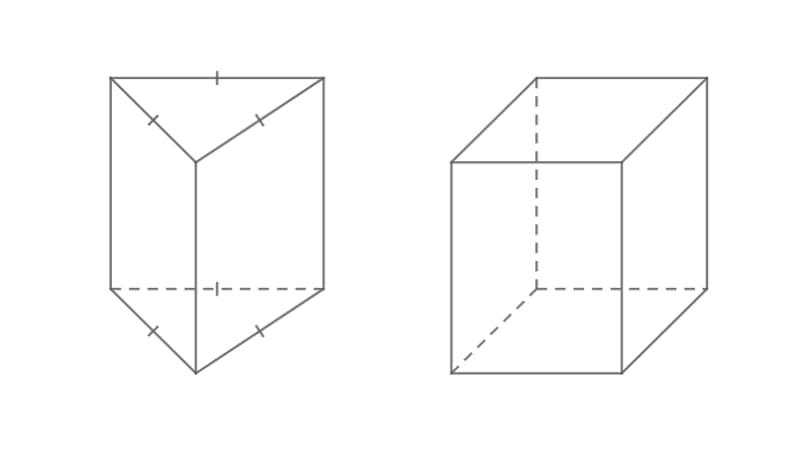Hình lăng trụ đều

Công Thức Liên Quan Đến Hình Lăng Trụ

Diện Tích Xung Quanh

Diện tích xung quanh của hình lăng trụ đứng bằng chu vi đáy nhân với chiều cao: Sxq = p.h (p là chu vi đáy, h là chiều cao).

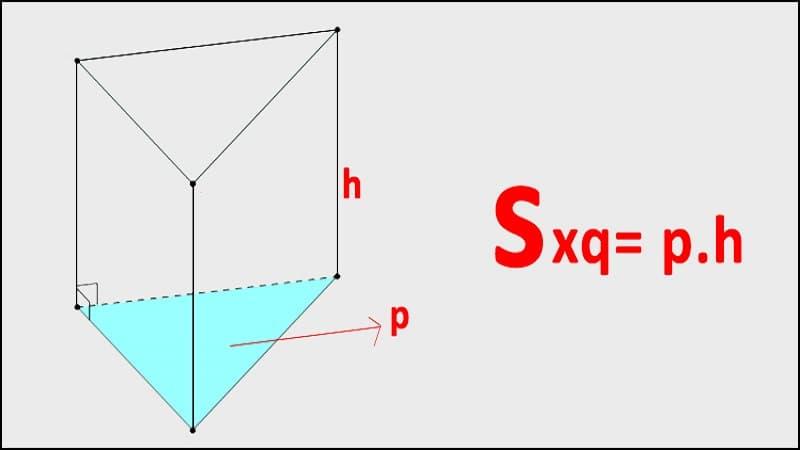Diện tích xung quanh

Diện Tích Toàn Phần

Diện tích toàn phần của hình lăng trụ bằng diện tích xung quanh cộng với diện tích hai đáy: Stp = Sxq + 2.Sđáy.

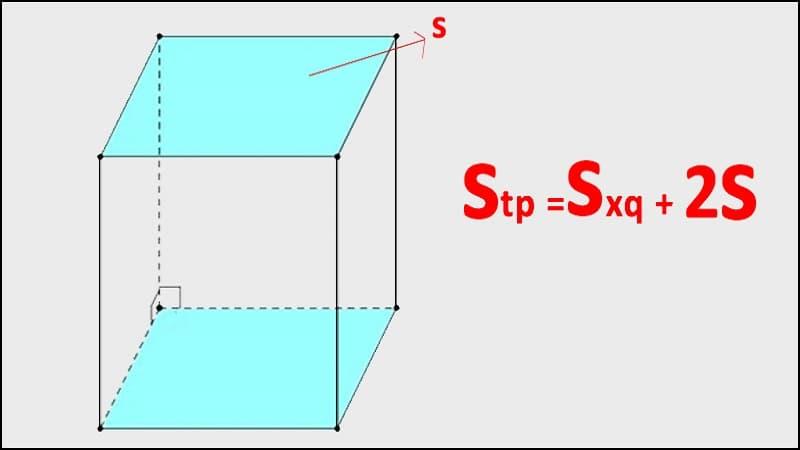Diện tích toàn phần

Thể Tích Khối Lăng Trụ

Thể tích khối lăng trụ bằng diện tích đáy nhân với chiều cao: V = Sđáy x h.

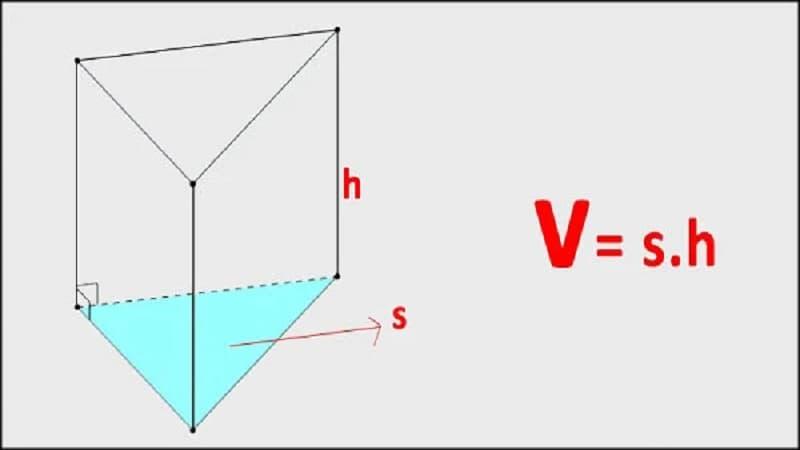Thể tích khối lăng trụ

Nếu bạn là người yêu động vật, việc tìm hiểu chó ỉa ra máu là bị bệnh gì là rất cần thiết.

Một Số Dạng Hình Lăng Trụ Đặc Biệt

Hình Hộp Đứng

Hình hộp đứng là hình hộp có cạnh bên vuông góc với mặt đáy. Mặt đáy là hình bình hành và các mặt bên là hình chữ nhật.

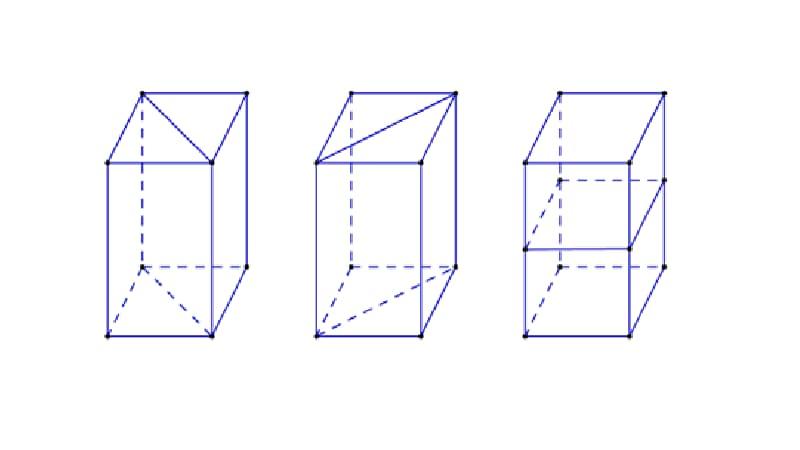Hình hộp đứng

Hình Hộp Chữ Nhật

Hình hộp chữ nhật là hình hộp có tất cả 6 mặt đều là hình chữ nhật. Nó có 12 cạnh, 8 đỉnh và 6 mặt.

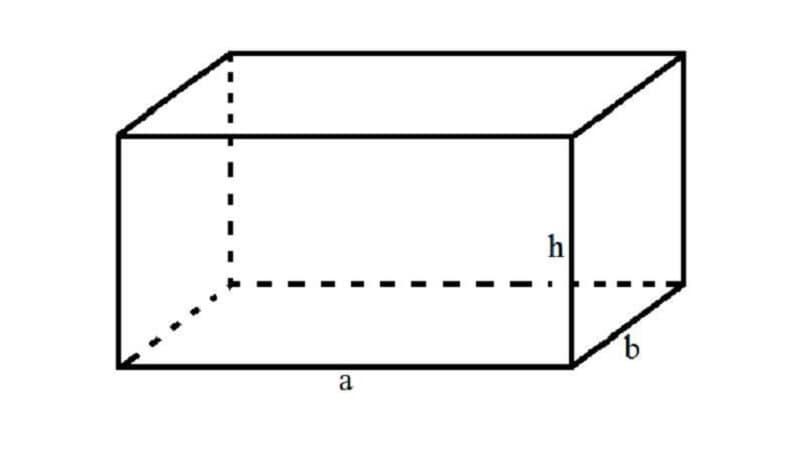Hình hộp chữ nhật

Hình Lập Phương

Hình lập phương là hình hộp chữ nhật có tất cả các mặt đều là hình vuông. Mỗi đỉnh là đỉnh chung của ba mặt.

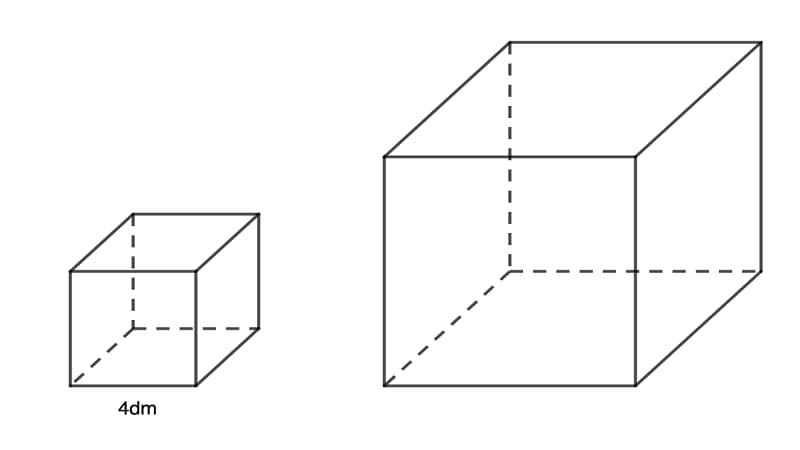Hình lập phương

Bạn có biết nhân sinh như kịch, người tản kịch tàn nghĩa là gì không?

Bài Tập Về Khối Lăng Trụ

Bài 1

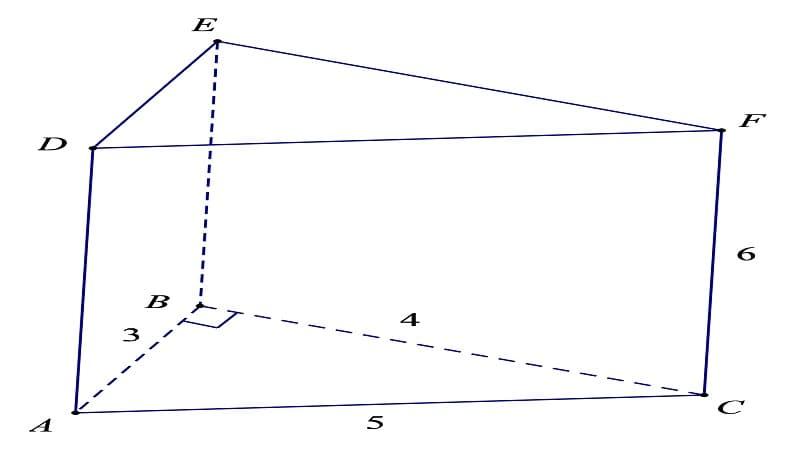
Chu vi đáy tam giác ABC là 12cm, chiều cao là 6cm. Diện tích xung quanh hình lăng trụ ABCDEF là 12 x 6 = 72cm². Diện tích đáy là 6cm². Thể tích hình lăng trụ ABCDEF là 6 x 6 = 36cm³.

Bài 2

Chu vi đáy là 2.(1+3) = 8cm, chiều cao là 5cm. Diện tích xung quanh là 8 x 5 = 40cm². Diện tích đáy là 3 x 1 = 3cm². Thể tích hình lăng trụ là 3 x 5 = 15cm³.

Việc phân biệt ngôi kể thứ nhất là gì ngôi kể thứ ba là gì cũng rất quan trọng trong việc học văn.

Bài 3

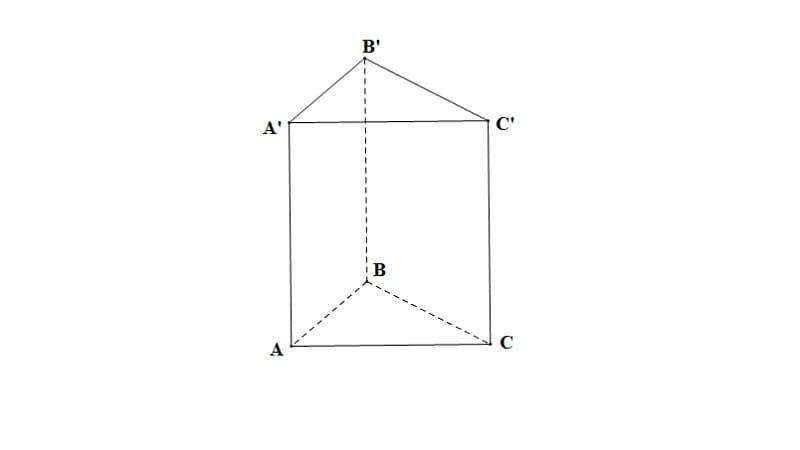
Hình lăng trụ đứng tam giác có 9 cạnh.

Bài 4

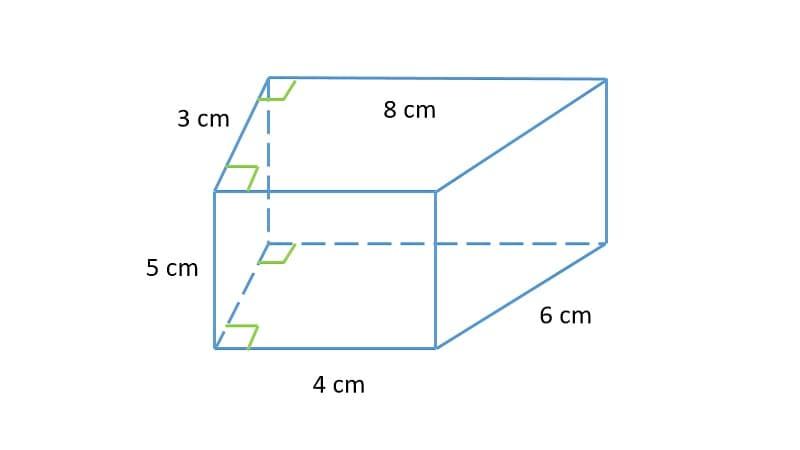
Diện tích đáy hình thang là ½.(4+8).3 = 18cm². Thể tích hình lăng trụ là 18 x 5 = 90cm³.

Ung thư là gì? Đây là một căn bệnh nguy hiểm mà chúng ta cần tìm hiểu để phòng tránh.

Bài 5

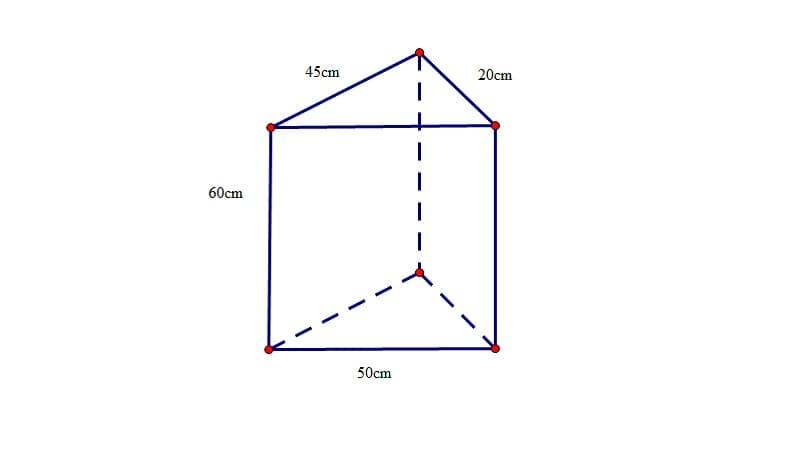
Diện tích xung quanh hình lăng trụ đứng tam giác là (45+20+50) x 60 = 6900cm².