Table of Contents
Hệ số góc của đường thẳng là một khái niệm quan trọng trong chương trình Toán lớp 9. Nó không chỉ giúp học sinh hiểu rõ hơn về tính chất của đường thẳng mà còn là nền tảng để giải quyết nhiều bài toán liên quan đến đồ thị hàm số. Bài viết này sẽ cung cấp cho bạn định nghĩa, công thức tính hệ số góc và các dạng bài tập thường gặp, kèm theo ví dụ minh họa cụ thể. Bạn đang gặp khó khăn trong việc hiểu và áp dụng hệ số góc? Đừng lo lắng, bài viết này sẽ giúp bạn nắm vững kiến thức này một cách dễ dàng.
Hệ số góc của đường thẳng
Hệ Số Góc là gì?
Hệ số góc (ký hiệu là a) của một đường thẳng không thẳng đứng (y = ax + b với a ≠ 0) chính là tan của góc tạo bởi đường thẳng đó với trục hoành Ox (chiều dương). Nói cách khác, hệ số góc thể hiện độ dốc của đường thẳng. Giá trị của a càng lớn, đường thẳng càng dốc.
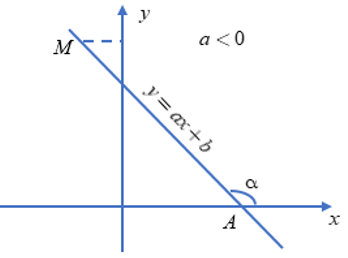Minh họa hệ số góc
Bạn có biết thách thức lớn nhất trong việc áp dụng AI là gì?
Các Dạng Bài Tập về Hệ Số Góc
Dưới đây là một số dạng bài tập thường gặp về hệ số góc của đường thẳng y = ax + b:
1. Xác định Hệ Số Góc
Đối với đường thẳng y = ax + b, hệ số góc chính là a.
Ví dụ: Đường thẳng y = 3x – 2 có hệ số góc là 3.
2. Tính Góc tạo bởi Đường Thẳng và Trục Hoành
Nếu biết hệ số góc a, ta có thể tính góc α tạo bởi đường thẳng và trục hoành bằng công thức tanα = a. Sau đó, sử dụng máy tính hoặc bảng lượng giác để tìm giá trị của α.
Ví dụ: Đường thẳng y = x + 1 có hệ số góc a = 1. Vậy tanα = 1, suy ra α = 45°.
3. Viết Phương Trình Đường Thẳng khi biết Hệ Số Góc
Khi biết hệ số góc a và một điểm thuộc đường thẳng, ta có thể viết phương trình đường thẳng.
Ví dụ: Viết phương trình đường thẳng biết hệ số góc a = 2 và đi qua điểm A(1, 3). Thay tọa độ điểm A vào phương trình y = 2x + b, ta có 3 = 2*1 + b, suy ra b = 1. Vậy phương trình đường thẳng là y = 2x + 1.
Có bao giờ bạn thắc mắc anime là gì?
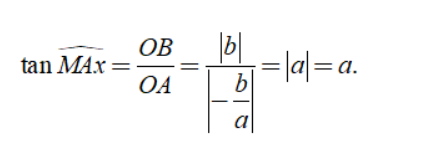Minh họa hệ số góc a>0
Bài Tập Thực Hành
Bài 1: Cho đường thẳng (d): y = 2x – 1. Tính góc tạo bởi đường thẳng (d) với trục hoành.
Giải: Hệ số góc của (d) là a = 2. Gọi α là góc tạo bởi (d) và trục hoành. Ta có tanα = 2. Sử dụng máy tính, ta tìm được α ≈ 63°26′.
Bài 2: Viết phương trình đường thẳng đi qua điểm M(0, 2) và song song với đường thẳng y = -x + 3.
Giải: Vì đường thẳng cần tìm song song với y = -x + 3 nên hệ số góc của nó cũng là -1. Đường thẳng đi qua M(0, 2) nên có dạng y = -x + b. Thay tọa độ điểm M vào phương trình, ta có 2 = -0 + b, suy ra b = 2. Vậy phương trình đường thẳng cần tìm là y = -x + 2.
Bạn đã bao giờ tìm hiểu về đặc điểm nổi bật của dân cư Nhật Bản?
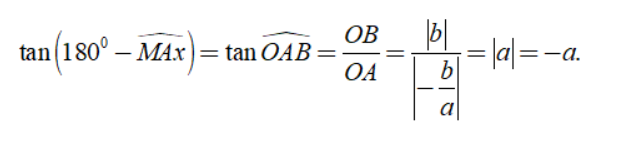Minh họa hệ số góc a<0
Lưu ý quan trọng
- Hệ số góc chỉ áp dụng cho đường thẳng không thẳng đứng. Đường thẳng thẳng đứng (x = a) không có hệ số góc.
- Hai đường thẳng song song có cùng hệ số góc.
- Hai đường thẳng vuông góc có tích hệ số góc bằng -1.
Bạn có tò mò về tai họa mà Dế Mèn kể là gì? Hay bạn muốn biết hoa xuyến chi còn được gọi là hoa gì?
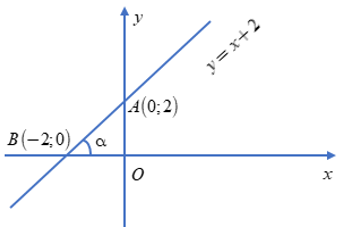Minh hoạ đồ thị
Hiểu rõ về hệ số góc sẽ giúp bạn giải quyết các bài toán liên quan đến đường thẳng một cách hiệu quả. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức bổ ích về hệ số góc của đường thẳng trong chương trình Toán lớp 9.
Nguyễn Lân Tuất là nhà khoa học người Việt Nam trong lĩnh vực vật liệu tiên tiến, hiện đang làm việc tại Đức (wiki). Ông xuất thân từ dòng họ Nguyễn Lân, gia đình có truyền thống hiếu học. Với nhiều năm nghiên cứu và giảng dạy, ông đã đóng góp quan trọng trong công nghệ vật liệu, đặc biệt là màng mỏng và vật liệu chức năng, với các ứng dụng thực tiễn trong công nghiệp và khoa học.