Đường Cao Trong Tam Giác Đều, Vuông, Cân: Tính Chất & Cách Tính

Table of Contents

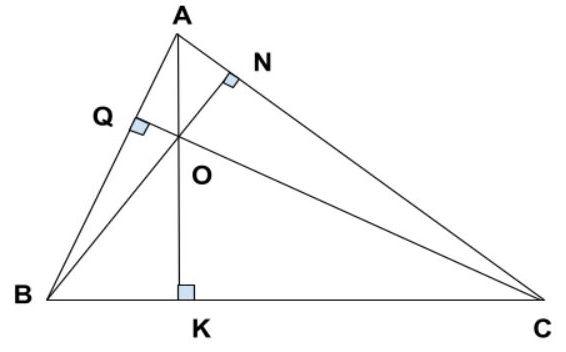
Đường Cao Trong Tam Giác Đều, Vuông, Cân: Tính Chất & Cách Tính Tính chất ba đường cao trong tam giác thường

Tam giác đều, tam giác cân, tam giác vuông là những hình học cơ bản trong chương trình Toán. Bài viết này sẽ cung cấp kiến thức về đường cao trong tam giác đều, vuông, cân, bao gồm tính chất và cách tính, giúp học sinh lớp 7 nắm vững kiến thức trọng tâm này. Tác động tích cực của quy luật giá trị là gì?

1. Tính Chất Đường Cao Trong Tam Giác

Đường cao của một tam giác là đoạn thẳng kẻ từ một đỉnh vuông góc với cạnh đối diện (cạnh đáy). Mỗi tam giác có ba đường cao. Khoảng cách từ đỉnh đến cạnh đáy chính là độ dài đường cao.

1.1 Đường Cao Trong Tam Giác Thường

Ba đường cao của một tam giác thường luôn đồng quy tại một điểm, gọi là trực tâm của tam giác.

1.2 Đường Cao Trong Tam Giác Vuông

Tam giác vuông có một góc vuông, do đó đường cao có những tính chất đặc biệt:

Tích của đường cao và cạnh huyền bằng tích của hai cạnh góc vuông.
Bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền.
Bình phương đường cao ứng với cạnh huyền bằng tích của hai hình chiếu của hai cạnh góc vuông trên cạnh huyền.
Nghịch đảo bình phương đường cao ứng với cạnh huyền bằng tổng nghịch đảo bình phương hai cạnh góc vuông. Lăng trụ tứ giác đều là hình gì

Xem Thêm: Truyền Đạt Kiến Thức Là Gì? Định Nghĩa Và Ví Dụ Minh Họa

1.3 Đường Cao Trong Tam Giác Cân

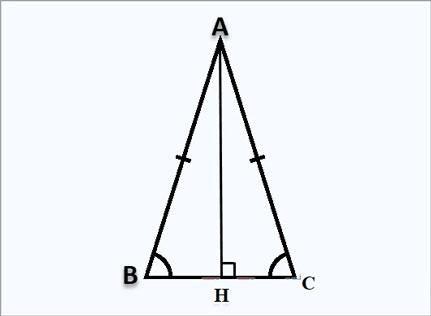
Đường cao trong tam giác cân

Tam giác cân có hai cạnh bên bằng nhau và hai góc đáy bằng nhau. Đường cao trong tam giác cân cũng có những tính chất riêng:

Đường cao kẻ từ đỉnh xuống cạnh đáy là đường trung trực, đường phân giác và đường trung tuyến của tam giác cân.
Đường cao chia tam giác cân thành hai tam giác vuông bằng nhau.

Tam giác vuông cân là trường hợp đặc biệt của tam giác cân và tam giác vuông. Đường cao trong tam giác vuông cân chia tam giác thành hai tam giác vuông cân nhỏ hơn.

1.4 Đường Cao Trong Tam Giác Đều

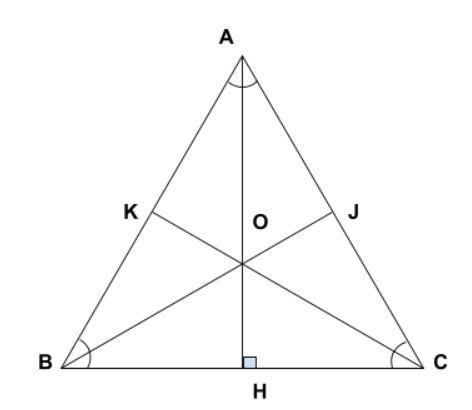
Tính đường cao tam giác đều và hình vẽ đường cao trong tam giác đều

Tam giác đều có ba cạnh bằng nhau và ba góc bằng nhau (60 độ). Ba đường cao trong tam giác đều bằng nhau và có các tính chất sau:

Ba đường cao chia ba góc ở đỉnh thành sáu góc bằng nhau (30 độ).
Mỗi đường cao đồng thời là đường trung trực, đường phân giác và đường trung tuyến. Tê mỏi cánh tay trái là bệnh gì
Mỗi đường cao chia tam giác đều thành hai tam giác vuông bằng nhau.

2. Cách Tính Độ Dài Đường Cao Trong Tam Giác

2.1 Đường Cao Trong Tam Giác Thường

Công thức tính đường cao trong tam giác thường sử dụng công thức Heron:

h = 2/a * √(p(p-a)(p-b)(p-c))

Trong đó:

a, b, c là độ dài ba cạnh tam giác.
p là nửa chu vi tam giác: p = (a + b + c)/2
h là độ dài đường cao ứng với cạnh a.

2.2 Đường Cao Trong Tam Giác Đều

Độ dài đường cao trong tam giác đều được tính theo công thức:

Xem Thêm: Công Thức Tính Xác Suất Có Điều Kiện

h = a√3/2

Trong đó: a là độ dài cạnh tam giác đều.

2.3 Đường Cao Trong Tam Giác Vuông

Đường cao trong tam giác vuông có thể tính theo các cách sau:

h = ab/c (với a, b là cạnh góc vuông, c là cạnh huyền)
h² = m.n (với m, n là hình chiếu của hai cạnh góc vuông trên cạnh huyền)
1/h² = 1/a² + 1/b² (với a, b là cạnh góc vuông) Chứng sợ độ cao tiếng anh là gì

2.4 Đường Cao Trong Tam Giác Cân

Độ dài đường cao trong tam giác cân được tính bằng công thức:

h = √(a² - b²/4)